Heap Sort
- 최대 힙 트리나 최소 힙 트리를 이용해 정렬을 하는 방법
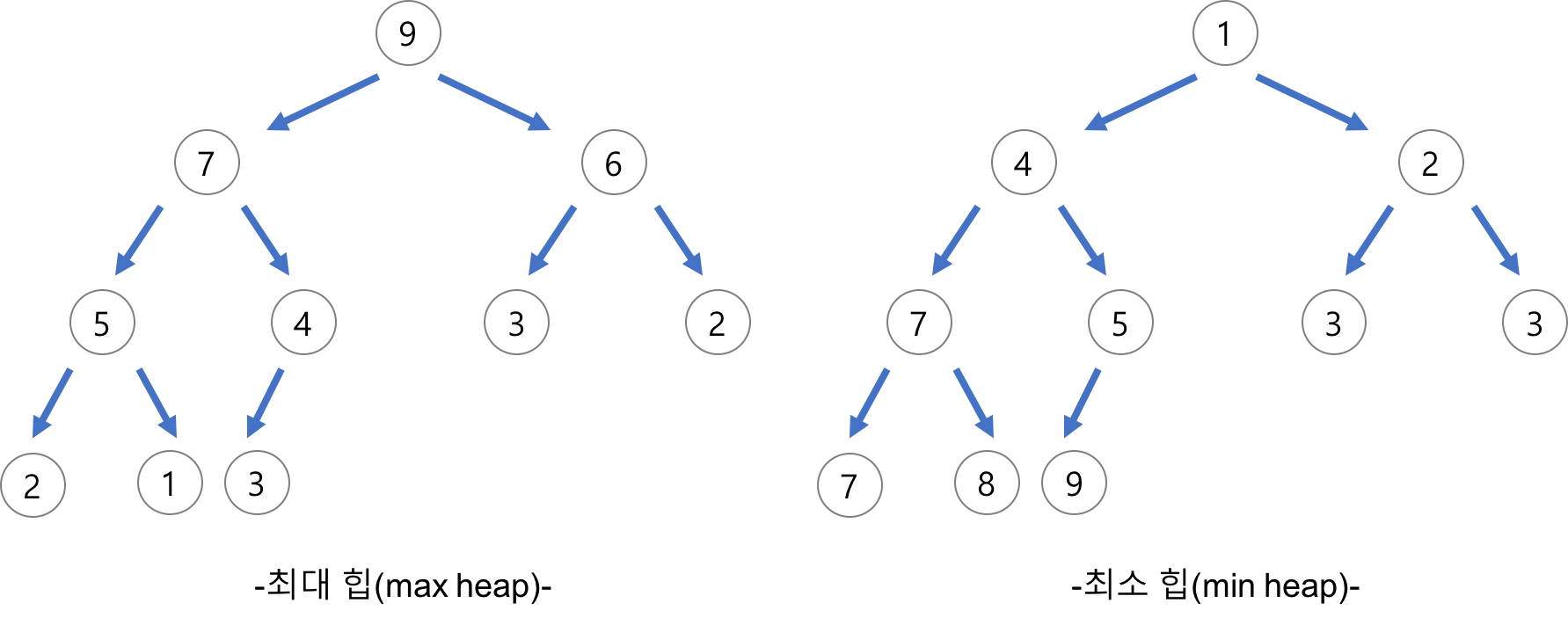
- heap : 반정렬 상태 ( 부모노드 >= 자식노드 or 부모노드 <= 자식노드)를 만족하는 완전 이진트리
- 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 된다.
- 과정 설명
1. 정렬해야 할 n개의 요소들로 최대 힙(완전 이진 트리 형태)을 만든다.
2. 내림차순을 기준으로 정렬
3. 그 다음으로 한 번에 하나씩 요소를 힙에서 꺼내서 배열의 뒤부터 저장하면 된다
4. 삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게
Max Heap 삽입
- 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모 노드들과 교환해서 힙의 성질 (반정렬상태)을 만족시킨다.
Max Heap 삭제
- 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
- 최대 힙(max heap)에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.
- 삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
- 힙을 재구성한다.
시간 복잡도
- worst : O(nlogn)
- average : O(nlogn)
- best : O(nlogn)
예시코드
//heap sort
#include <iostream>
#include <vector>
#define MAX_SZIE 11
using namespace std;
void heapInsert(vector<int>& arr, int val);
int heapRemove(vector<int>& arr);
int main() {
vector<int> minHeap;
for (int i = 0; i < MAX_SZIE; i++) {
int random = (601 * (i + 3)) % 271;
heapInsert(minHeap, random);
}
for (int i = 0; i < MAX_SZIE; i++) {
cout << heapRemove(minHeap) << " ";
}
cout << endl;
return 0;
}
void heapInsert(vector<int>& arr, int val) {
arr.push_back(val);
int idx = arr.size() - 1;
//heapify_up
do {
int parIdx = idx / 2;
if (arr[parIdx] > arr[idx]) {
swap(arr[parIdx], arr[idx]);
idx = parIdx;
}
else {
break;
}
} while (idx > 0);
}
int heapRemove(vector<int>& arr) {
int res = arr[0];
swap(arr[0], arr[arr.size() - 1]);
arr.pop_back();
int idx = 0;
//heapify_down
do {
int left = (idx * 2) + 1;
int right = (idx * 2) + 2;
if (right < arr.size()) { // 자식 2개 존재
int small = arr[left] < arr[right] ? left : right; // 둘 중 더 작은 자식
if (arr[small] < arr[idx]) { // 작은 자식이 부모 보다 더 작은 경우
swap(arr[small], arr[idx]);
}
idx = small;
}
else if (left < arr.size() && arr[left] < arr[idx]) { //자식 1개 존재
// 자식이 더작은 경우
swap(arr[left], arr[idx]);
idx = left;
}
else { //자식이 없거나 자식 있어도 더 자식 값이 더 큰 경우
break;
}
} while (idx < arr.size());
return res;
}
'CS > Algorithm' 카테고리의 다른 글
| 탐색2 : Hashing (0) | 2020.02.25 |
|---|---|
| 탐색1 : 선형탐색, 이진탐색 (0) | 2020.02.25 |
| 정렬2 : 분할정복을 이용한 정렬 (0) | 2020.02.25 |
| 정렬1 : 기초정렬 (0) | 2020.02.25 |
| 다이나믹 프로그래밍 (0) | 2020.02.21 |
