selection sort
insertion sort
bubble sort
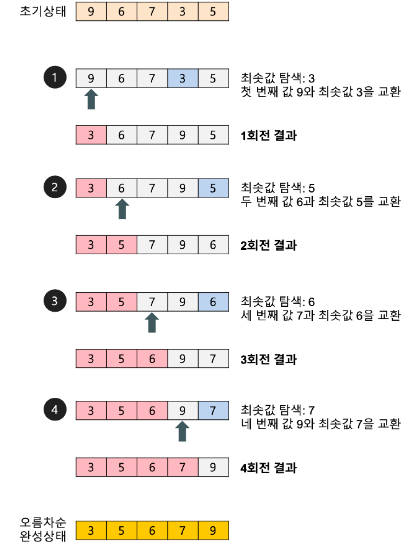
Selection Sort
제자리 정렬(in-place sorting) 알고리즘의 하나
입력 배열(정렬되지 않은 값들) 이외에 다른 추가 메모리를 요구하지 않는 정렬 방법
해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘
첫 번째 순서에는 첫 번째 위치에 가장 최솟값을 넣는다.
두 번째 순서에는 두 번째 위치에 남은 값 중에서의 최솟값을 넣는다.
과정 설명
주어진 배열 중에서 최솟값을 찾는다.
그 값을 맨 앞에 위치한 값과 교체한다(패스(pass)).
맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
하나의 원소만 남을 때까지 위의 1~3 과정을 반복한다.
time complexity
worst : O(n^2)
average : O(n^2)
best : O(n^2)
//selection sort
#include <iostream>
#include <vector>
using namespace std;
void selectionSort(vector<int>& arr);
int main() {
vector<int> arr;
arr.push_back(9);
arr.push_back(6);
arr.push_back(7);
arr.push_back(3);
arr.push_back(5);
for(int n=0; n<arr.size(); n++){
cout << arr[n] << " "; // 9 6 7 3 5
}
selectionSort(arr);
cout << endl;
for(int n=0; n<arr.size(); n++){
cout << arr[n] << " "; // 3 5 6 7 9
}
}
void selectionSort(vector<int>& arr){
int min, minIdx, swap ;
for(int i=0; i<arr.size(); i++){
min = arr[i];
for(int j=i+1; j<arr.size(); j++){
if(min > arr[j]){
min = arr[j];
minIdx = j;
}
}
swap = arr[i];
arr[i] = arr[minIdx];
arr[minIdx] = swap;
}
}
Insertion Sort
정의
자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘
과정 설명
삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬 즉, 두 번째 자료는 첫 번째 자료, 세 번째 자료는 두 번째와 첫 번째 자료, 네 번째 자료는 세 번째, 두 번째, 첫 번째 자료와 비교한 후 자료가 삽입될 위치를 찾는다. 자료가 삽입될 위치를 찾았다면 그 위치에 자료를 삽입하기 위해 자료를 한 칸씩 뒤로 이동시킨다.
처음 Key 값은 두 번째 자료부터 시작한다.
time complexity
worst : O(n^2)
average : O(n^2)
best : O(n)
//insertion sort
#include <iostream>
#include <vector>
using namespace std;
void insertionSort(vector<int>& arr);
int main() {
vector<int> arr;
arr.push_back(9);
arr.push_back(6);
arr.push_back(7);
arr.push_back(3);
arr.push_back(5);
for(int n=0; n<arr.size(); n++){
cout << arr[n] << " "; // 9 6 7 3 5
}
insertionSort(arr);
cout << endl;
for(int n=0; n<arr.size(); n++){
cout << arr[n] << " "; // 3 5 6 7 9
}
}
void insertionSort(vector<int>& arr){
int key, i , val;
for(i=1; i<arr.size(); i++){
key = i-1;
while(key >= 0 && arr[key] > arr[i]){
key--;
}
val = arr[i];
arr.erase(arr.begin()+i);
arr.insert(arr.begin()+key+1, val);
}
}
Bubble Sort
bubble sort
정의
서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
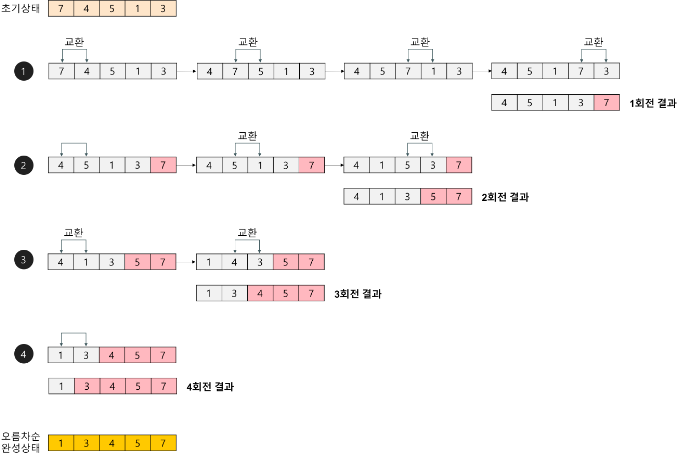
과정 설명
버블 정렬은 첫 번째 자료와 두 번째 자료를, 두 번째 자료와 세 번째 자료를, 세 번째와 네 번째를, … 이런 식으로 (마지막-1) 번째 자료와 마지막 자료를 비교하여 교환하면서 자료를 정렬한다. 1회전을 수행하고 나면 가장 큰 자료가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 자료는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 두 번째 자료까지는 정렬에서 제외된다. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어난다.
time complexity
worst : O(n^2)
average : O(n^2)
best : O(n)
//bubble sort
#include <iostream>
#include <vector>
using namespace std;
void bubbleSort(vector<int>& arr);
int main() {
vector<int> arr;
arr.push_back(9);
arr.push_back(6);
arr.push_back(7);
arr.push_back(3);
arr.push_back(5);
for(int n=0; n<arr.size(); n++){
cout << arr[n] << " "; // 9 6 7 3 5
}
bubbleSort(arr);
cout << endl;
for(int n=0; n<arr.size(); n++){
cout << arr[n] << " "; // 3 5 6 7 9
}
}
void bubbleSort(vector<int>& arr){
for(int i=arr.size(); i>=1; i--){
for(int j=0; j<i-1; j++){
if(arr[j+1] < arr[j]){
int swap = arr[j+1];
arr[j+1] = arr[j];
arr[j] = swap;
}
}
}
}