문자열 매칭 알고리즘

1. 단순 문자열 매칭
2. KMP (Knuth-Morris-Pratt) 알고리즘
3. Boyer-Moore 알고리즘

kmp

 

 

단순 문자열 매칭 알고리즘

• 문자 하나씩 확인하는 알고리즘으로 가장 간단한 형태의 알고리즘
• 의사코드
  • 전체 문자열의 첫번째 문자에서 시작하여 찾을 문자열의  첫번째 문자를 비교
  • 매칭이 이루어지면 찾을 문자열의 다음 문자를 비교
  • 매칭이 이루어지지 않으면 전체 문자열의 두번째 문자에서 다시 시작
  • 위의 과정을 반복하여 문자열을 찾는다
• 시간 복잡도 : O(N*M) // N = 전체 문자열 길이, M = 찾을 문자열 길이

 

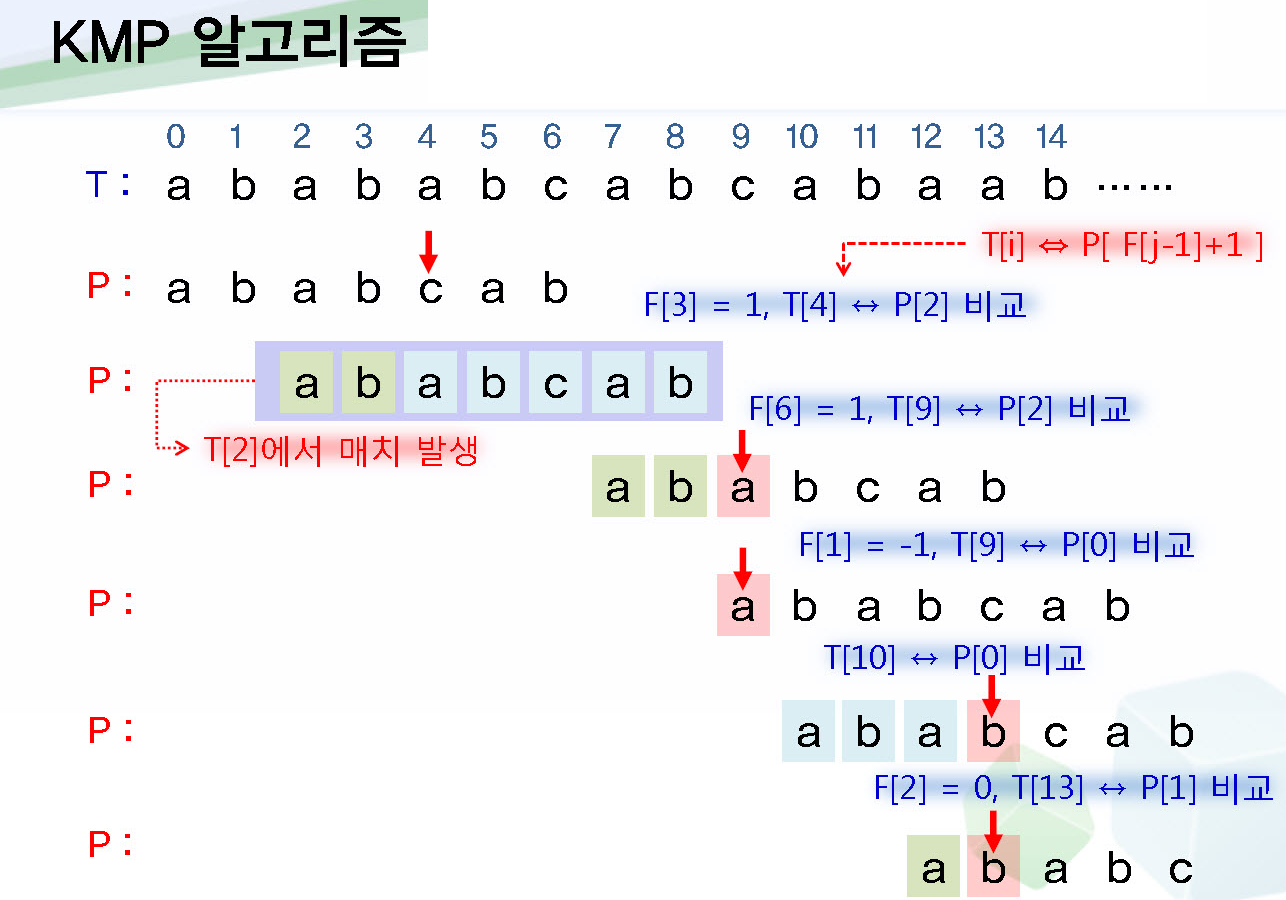
KMP (Knuth-Morris-Pratt) 알고리즘

• 접두사와 접미사의 개념을 활용하여 '반복되는 연산을 얼마나 줄일 수 있는지 판별'하고 매칭할 문자열을 빠르게 점프하는 기법
• 접두사 : 찾을 문자열의 앞에 있는 문자열
• 접미사 : 찾을 문자열의 뒤에 있는 문자열
• 경계(border) : 접두사와 접미사가 일치하는 쌍
• 의사코드
  • 전체 문자열의 첫번째 문자부터 찾을 문자열과 비교시작
  • 매칭이 이루어지지 않은 문자가 발견되면, 발견되기 전까지 전체 문자열과 일치했던 찾을 문자열의 경계를 구한다.
  • 찾을 문자열의 접두사를 전체 문자열의 접미사로 점프하여 비교를 재개
• 시간 복잡도 : O(N) // N = 전체 문자열 길이
• 경계를 찾는데 소요되는 비용은 공짜가 아니므로, 검색을 수행하는 중간에 매번 경계를 찾는것은 고비용
  => 검색을 수행하기 전에 미리 찾을 문자열로 부터 경계의 정보를 갖는 "테이블"을 생성
  • 테이블 인덱스 : 일치 접두부의 길이
  • 테이블 원소 : 일치 접두부의 최대 경계 너비 (첫번째 문자는 일치 접두부가 존재하지 않으므로 항상 -1)
  • 매칭 불일치시 이동 거리 = 일치 접두부의 길이 - 최대경계너비

 

Boyer-Moore 알고리즘

• 오른쪽에서 왼쪽으로 비교하고 이동은 왼쪽으로 오른쪽으로 하는 방식
• 오른쪽 끝에 문자가 일치 하지 않고 해당 본문 문자가 패턴에 존재하지 않으면 패턴 길이만큼 이동